Abbildung 1
A) Einleitung
Die zunehmende Durchdringung unserer Welt mit Computern macht auch vor der Schule nicht halt: es gibt kaum ein Schulfach, für
das die Didaktiker nicht über die spezifischen Möglichkeiten des Computereinsatzes nachdenken. Für jedes Unterrichtsthema ist zu entscheiden, ob der Einsatz des Computers sinnvoll ist oder nicht. Eine dabei hilfreiche Regel lautet: Der Computer sollte nur dann eingesetzt werden, wenn man mit seiner Hilfe etwas erreichen kann, das man ohne ihn überhaupt nicht oder nur mit unverhältnismäßig größerem Aufwand erreichen könnte.
Für viele Jahrhunderte waren Zirkel und Lineal durchaus ausreichende Werkzeuge für alle, die Geometrie betreiben wollten. Für den Anfangsunterricht in der Geometrie halte ich deren handgreiflichen Einsatz auch nach wie vor für unbedingt notwendig: jeder Schüler muß sich die Welt der Geometrie zunächst mit Hilfe seiner Hände erarbeiten! Wenn wir unsere Schüler zu früh mit einem Geometrieprogramm arbeiten lassen, laufen wir Gefahr, dass sie die elementaren Objekte und Strukturen der Geometrie noch nicht genügend "begriffen" (welch ein schönes Wort!) haben. Daher sollte die Erarbeitung elementarer Begriffe wie Strecke, Gerade, Kreis, parallel, orthogonal, schneiden usw. völlig ohne Computereinsatz durchgeführt werden. Der Einsatz von Geometriesoftware ist erst sinnvoll, wenn kompliziertere Beziehungen zwischen verschiedenen Teilen einer Konstruktion thematisiert werden. Konkret bedeutet das für meinen eigenen Geometrieunterricht: frühestens bei der Behandlung des Thalessatzes.
Die Möglichkeit, eine geometrische Zeichnung auf dem Bildschirm statt auf einem Blatt Papier zu erstellen, ist alleine sicher
noch keine ausreichende didaktische Begründung für den Einsatz eines "dynamischen" Geometrieprogramms (kurz DGS). Solche Programme bieten aber darüberhinaus die Möglichkeit, die gegenseitige Lage der Objekte einer Zeichnung nachträglich zu verändern, ohne dass dabei der durch die Konstruktion festgelegte geometrische Zusammenhang zwischen ihnen verloren geht. Dieses wohl faszinierendste Detail aller Programme zur "beweglichen Geometrie" wird gewöhnlich Zugmodus genannt. Der Zugmodus erlaubt also, die vorliegende Zeichnung als eine
ganze "Klasse" von Zeichnungen zu verstehen, wobei sich die einzelnen Varianten der Zeichnung in der konkreten Lage der
geometischen Objekte unterscheiden und es trotzdem eine für alle Varianten gültige Konstruktionsbeschreibung gibt.
Die obige Verwendung des Begriffes "Klasse" deutet an, wie man die Veränderung der didaktischen Situation beim Einsatz eines Dynamischen Geometrieprogramms mit den Begriffen der modernen Informatik beschreiben kann:
Durch Variation über die Instanzen ("Ziehen der Zeichnung") kann man Eigenschaften der Konstruktion erkennen; diese zeigen sich nämlich als Invarianten im Zugmodus. So ist zum Beispiel die Tatsache, dass sich die drei Höhen eines Dreiecks in genau einem Punkt schneiden, eine Eigenschaft der Konstruktion und nicht (nur) der jeweiligen Zeichnung: ist die Konstruktion korrekt durchgeführt worden, dann schneiden sich die drei Höhen stets in einem Punkt, wie auch immer ich meine Zeichnung "verziehe". Der Einsatz des DGS begünstigt und erleichert das Wahrnehmen dieser Invarianten.
Neben dem Zugmodus haben die dynamischen Geometrieprogramme noch zwei weitere charakteristische Fähigkeiten: sie sind "lernfähig" in dem (eingeschränkten) Sinne, dass sich komplexere Befehlsfolgen zu Makros zusammenfassen lassen, und sie erlauben die Aufzeichnung von Punktbahnen, im einfachsten Fall als Spuren, die der Punkt beim Ziehen der Zeichnung hinterläßt, oft aber als sogenannte Ortslinien, welche im besten Falle ebenfalls am Zugmodus teilnehmen, d.h. ihre Lage dynamisch verändern.
Man kann ein Computerprogramm natürlich benutzen, ohne zu verstehen, nach welchen Prinzipien es gebaut ist und funktioniert. Für diejenigen aber, die gerne mal einen Blick hinter die Kulissen werfen wollen, bietet sich die Gelegenheit dazu nicht gerade oft. Im Falle von EUKLID DynaGeo sind die verwendeten Algorithmen und Datenstrukturen jedoch so einfach, dass sie jeder mathematisch Interessierte auch ohne spezielle Informatik-Kenntnisse zumindest in den Grundzügen verstehen kann. Im folgenden möchte ich zunächst zeigen, mit welchen Datenstrukturen eine geometrische Konstruktion in EUKLID DynaGeo dargestellt wird. Sodann werde ich auf die Realisierung des Zugmodus, die Implementierung der Makros und die Aufzeichnung von Ortslinien eingehen. Nach diesen informatischen Ausführungen will ich mit einem Beispiel für den sinnvollen und lohnenden Unterrichtseinsatz eines Dynamischen Geometrieprogramms schließen.
B) Interne Darstellung geometrischer Konstruktionen
EUKLID DynaGeo entstand 1994 aus dem Versuch, unter Windows die Funktionalität des damals nur für DOS verfügbaren Programms CABRI zur Verfügung zu stellen. Wie sein Vorbild beschränkt sich auch EUKLID DynaGeo auf die ebene Geometrie, und innerhalb dieses Rahmens im wesentlichen auf Punkte, Geraden (und Strecken!) sowie Kreise. Allerdings gibt es viele verschiedene Arten von Punkten, z.B.: "freie" Punkte, Schnittpunkte zweier Linien, Punkte auf einer Linie. Auch bei den geraden Linien gibt es viele Sorten, z.B.: "freie" Geraden, Geraden durch 2 Punkte, Lot von einem Punkt auf eine Gerade, Verbindungsstrecken von 2 Punkten. Und bei den Kreisen sieht es auch nicht viel übersichtlicher aus: "freie" Kreislinien, Kreise mit gegebenem Mittelpunkt und Radius, Kreise mit gegebenem Mittelpunkt durch einen anderen Punkt, Kreise durch 3 Punkte.
Um die Komplexität der gestellten Aufgabe bewältigen zu können, bietet sich die objektorientierte Programmierung an: jedem geometrischen Objekttyp entspricht ein Pascal-Objekttyp. Unter einem Objekt versteht man in der Informatik eine Zusammenfassung von Datenfeldern und auf diesen Datenfeldern operierenden Funktionen bzw. Prozeduren (in Pascal "Methoden" genannt) zu einer neuen Einheit. Die Kommunikation des Programms (und damit des Benutzers) mit dem Objekt soll dabei vollständig über die Methoden abgewickelt werden ("Kapselung"), was Seiteneffekte vermindert und zu stabileren Programmen führt.

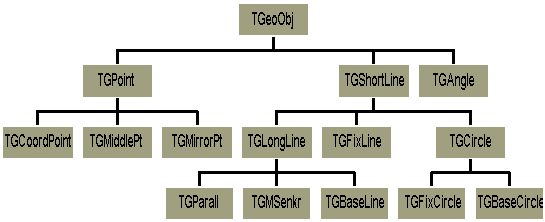
Die eigentliche Stärke von Objekten liegt jedoch in der Möglichkeit, einen neuen Typ aus einem schon vorhandenen abzuleiten, indem man einfach Datenfelder und Methoden hinzufügt oder schon vorhandene Methoden umdefiniert ("Vererbung"). Der Vorteil dabei ist, dass für jedes Objekt nur derjenige Anteil des Codes neu geschrieben werden muß, in dem sich dieses Objekt von seinem Vorfahren unterscheidet. Abbildung 1 zeigt einen Ausschnitt aus dem Stammbaum der in EUKLID DynaGeo implementierten geometrischen Objekte.
Ein "Urtyp" namens TGeoObj enthält alle Datenfelder, die jedes abgeleitete Objekt braucht, z.B. die Felder
Außerdem enthält er alle Methoden, über die jedes abgeleitete Objekt verfügen muß, z.B.
Alle abgeleiteten Objekttypen enthalten zusätzliche Datenfelder und Methoden oder auch neue Versionen von Methoden des Vorfahren ("überschriebene Methoden"). Zum Beispiel hat jeder Objekttyp seine eigenen Methoden "UpdateParams" und "DrawIt"; TGFixLine hat gegenüber TGShortLine ein zusätzliches Datenfeld "MyLength" in dem die (feste) Länge dieser Strecke abgelegt wird.
Um den größten Nutzen aus diesem Konzept zu ziehen, muß man also beim Entwurf der Objekttyphierarchie die Objekte so anordnen, dass die Summe der Unterschiede zwischen den abgeleiteten Objekten und ihren jeweiligen Vorfahren minimal wird. Z.B. unterscheiden sich der Objekttyp "TGMiddlePt" im wesentlichen nur in 3 Methoden ("Create", "UpdateParams" und "GetInfo") von seinem Vorfahren "TGPoint", obwohl total verschiedene geometrische Sachverhalte hinter den entsprechenden Objekten stecken. Die hier realisierte Hierarchie ist aber wahrscheinlich nicht optimal, weil ich zu ihrer Entwurfszeit noch keine hinreichenden Erfahrungen mit den projektierten Objekttypen hatte.
Wenn der Benutzer nun zur Laufzeit den Befehl zur Erzeugung eines Objekts gibt, wird eine Instanz des entsprechenden Pascalobjekts erzeugt und in eine Liste eingetragen, die den Konstruktionsgang chronologisch dokumentiert. Diese Objektliste stellt damit eine programm-interne Version der Konstruktionsbeschreibung für die vom Benutzer erzeugte Figur dar.
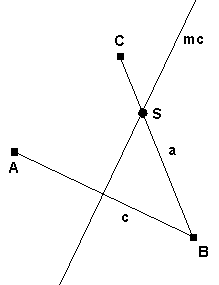
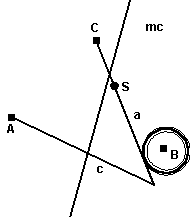
Betrachten wir als Beispiel die einfache Zeichnung von Abbildung 2. Der Zeichnung liegt folgende Konstruktion zugrunde:
Diese Konstruktionsbeschreibung enthält zum einen den chronologischen Ablauf der Konstruktion: Abbildung 3 zeigt die zur Laufzeit angelegte Objektliste, welche ebenfalls die "Geschichte" der Konstruktion enthält:

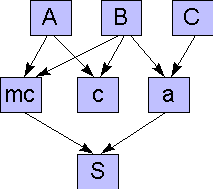
Die obige Konstruktionsbeschreibung enthält jedoch noch mehr als nur die Chronologie der Konstruktion, nämlich sämtliche Informationen über die logischen Abhängigkeiten der geometrischen Objekte voneinander. Eine Übersicht über diese gegenseitigen Abhängigkeiten erhält man durch eine netzartige Darstellung (Abbildung 4).
Man sieht z.B. dass der Schnittpunkt S direkt von mc und a abhängt, indirekt aber auch von allen drei Punkten A, B und C. Daraus folgt: ändert auch nur einer dieser drei Punkte seine Lage, dann wird auch S seine Lage ändern müssen. Andererseits ist zu erkennen, dass mc nicht neu gezeichnet werden muß, wenn C seine Lage verändert.
Zur Speicherung dieser logischen Abhängigkeiten führt jedes Objekt
Das "Netz der Verwandtschaften" erscheint also in der Objektliste in Form von Verweisen auf Eltern- und Kind-Objekte, wobei jede Abhängigkeit durch 2 Verweise dargestellt wird:
Abbildung 5 zeigt die Objektliste mit diesen Verweisen auf Eltern und Kinder:
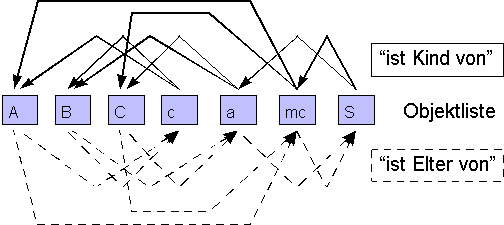
Eine Spezialität des Programms EUKLID DynaGeo sind die Strecken fester Länge. Diese Objekte sprengen das am Vorbild der Blutsverwandtschaft orientierte Schema logischer Abhängigkeiten: wenn Sie bei einer Strecke AB der festen Länge 3 cm den Punkt A verziehen, dann erwarten Sie mit Recht, dass der Punkt B im Abstand von 3 cm folgt. B ist dann also ein Kind von A. Wenn Sie sich nun aber entschieden hätten, an B statt an A zu ziehen, dann müßte A im Abstand von 3 cm hinter B herziehen - als Kind von B statt als Elter!
Zur Verwaltung dieses logischen Zusammenhangs wird eine neue Beziehung zwischen Punkten definiert: die Freundschaft. Zwei Punkte sind genau dann befreundet, wenn sie über eine Strecke fester Länge miteinander verbunden sind. Jeder Punkt führt neben der Eltern- und der Kinderliste eine weitere Liste, in der seine Freunde vermerkt sind. Befreundete Punkte sind normalerweise gleichberechtigt und unabhängig - bis zum Krisenfall, wenn einer aus dem Kreis der Freunde "gezogen" wird: dann wird der zum Anführer (d.h. zum temporären Elter) der anderen, die ihm im jeweils zugehörigen Abstand folgen. Am Ende dieses Zugvorgangs werden die temporären Eltern-Kind-Beziehungen wieder aufgelöst.
Eine weitere Art der temporären Verwandtschaft tritt bei der Bindung eines Punktes an eine Linie auf: der Punkt kann sich dann nur noch auf dieser Linie bewegen, seine Lage wird damit abhängig von der Lage der Linie, er selbst wird also zum Kind dieser Linie, welche ihn sozusagen "adoptiert". Falls der Benutzer die Bindung des Punktes an diese Linie wieder aufhebt, muß diese Adoption wieder rückgängig gemacht werden.
Durch diese temporären Verwandschaften wird die statische Hierarchie eines gewöhnlichen Stammbaums aufgebrochen: erst zu Beginn eines Zugvorgangs wird entschieden, von welchen Eltern ein Objekt in der gegenwärtigen Situation abhängt. Dies macht es ein wenig schwieriger, zirkuläre Verwandschaftsbeziehungen zu vermeiden, was aber unbedingt immer sichergestellt sein muß: wäre ein Objekt sein eigener Großvater (und damit gleichzeitig auch sein eigener Enkel!), dann würde der im nächsten Abschnitt beschriebene Algorithmus des Verziehens unvermeidlicherweise zu einer Endlosschleife führen.
C) Der Zugmodus
Wenden wir uns nun der ersten der charakteristischen Fähigkeiten dynamischer Geometrieprogramme zu, dem Zugmodus. Er wird in EUKLID DynaGeo nach den folgenden beiden Regeln realisiert:
Dabei ist "aktualisieren" ein dreistufiger Prozess:
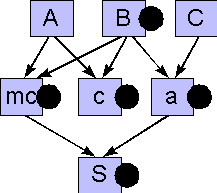
Als Beispiel soll in der in Abbildung 2 dargestellten Konstruktion jetzt der Punkt B gezogen werden. Zunächst werden alle vom Zugvorgang betroffenen Objekte markiert. Dies geschieht durch eine rekursive Prozedur: ein Objekt markiert sich selbst und ruft dann für alle seine Kinder dieselbe Markierungsprozedur auf. Abbildung 6 zeigt den dann erreichten Zustand; die Markierungen sind durch die schwarzen Punkte dargestellt.
Sodann werden alle vom Zugvorgang betroffenen Objekte aktualisiert. Auch dies geschieht durch eine rekursive Prozedur: ein Objekt testet zunächst, ob alle seine Eltern schon "fertig" sind; falls ja, dann aktualisiert es sich selbst, löscht (zum Zeichen, dass es "fertig" ist) seine Markierung und ruft dann für alle seine Kinder dieselbe Aktualisierungsprozedur auf.
 |
 |
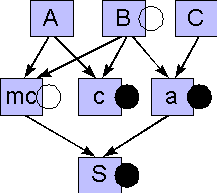
Die Abbildungen 7 und 8 zeigen den Zustand, nachdem sich B und das 1. Kind von B, nämlich mc, aktualisiert haben:
Beachten Sie, dass in Abbildung 8 mc nicht mehr Mittelsenkrechte von c ist, wohl aber Mittelsenkrechte der Strecke [AB]! Der Grund dafür ist, dass A, B, und mc sich schon aktualisiert haben, c jedoch noch nicht. Entsprechend liegt (der noch nicht aktualisierte Schnittpunkt) S zwar noch auf a, aber nicht mehr auf (der schon aktualisierten Mittelsenkrechten) mc. Während des Ziehens gerät also eine solche Zeichnung vorübergehend "außer Synchronisation", was man bei genügend umfangreichen Zeichnungen durchaus auch auf dem Bildschirm beobachten kann.
Als nächstes ruft mc seinerseits die Aktualisierungsroutine für S auf. S testet zunächst seine Eltern und stellt fest, dass noch nicht alle "fertig" sind. Also kehrt die Routine unverrichteter Dinge zurück zu mc. Dieses Objekt hat damit den gesamten Aktualisierungsprozess vollbracht und gibt seinerseits zurück an B. B ist dabei, seine Kinder zu aktualisieren und ruft als nächstes die Routine für c, dann für a auf. Nachdem a sich aktualisiert hat, erhält schließlich S einen nun ausführbaren Aktualisierungsauftrag von a.
Durch dieses Verfahren ist also gewährleistet, dass jedes Objekt bei der Nachfrage nach den Daten der Eltern stets schon aktualisierte Daten vorfindet, die es dann benutzen kann, um seine eigenen neuen Daten zu berechnen.
D) Die Makros
Die zweite charakteristische Fähigkeit dynamischer Geometriesoftware ist die Möglichkeit, den endlichen Befehlsvorrat des Programms nach den individuellen Wünschen des Anwenders zu erweitern: eine Folge von vorhandenen Befehlen kann zu einem neuen Makro-Befehl zusammengefaßt werden. Der Anwender kann damit dem Programm zwar nichts substanziell Neues beibringen; dies bleibt nach wie vor dem Programmierer vorbehalten. Ein Makro kann aber einen immer wiederkehrenden längeren Konstruktionsvorgang durch einen einzigen Befehl abkürzen. Das ist in vielen Fällen eine sehr nützliche und willkommene Arbeitshilfe.
Vom Standpunkt der Informatik aus sind EUKLID DynaGeo-Makros Funktionen, denen eine Liste von Startobjekten übergeben wird und die daraufhin eine Liste von Zielobjekten generieren und zurückgeben. Dabei müssen die Zielobjekte durch die Startobjekte vollkommen determiniert sein. Nur dann ist das Makro "transportabel", d.h. in allen beliebigen Zeichnungen anwendbar, solange diese nur die Startobjekte zur Verfügung stellen können.
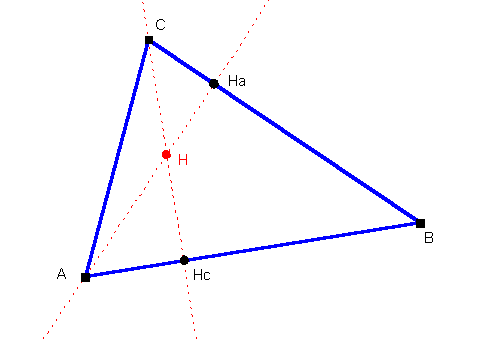
Als einfaches Beispiel soll hier die Aufzeichnung eines Makros "Konstruktion des Höhenschnittpunktes eines Dreiecks" betrachtet werden. Die Lage des Höhenschnittpunktes H ist durch die Positionen der drei Eckpunkte A, B und C des Dreiecks eindeutig festgelegt. Diese drei Punkte sind also die Startobjekte; der Höhenschnittpunkt ist das Zielobjekt.
Zunächst brauchen wir eine Zeichnung, die schon einmal vollständig die im Makro abzuspeichernde Konstruktion enthält (siehe Abbildung 9). Statt einer symbolischen Objektliste ist hier die von EUKLID DynaGeo für diese Konstruktion automatisch generierte Konstruktionsbeschreibung aufgelistet:
 |
A ist ein freier Basispunkt |
Ruft der Anwender nun in EUKLID DynaGeo den Befehl "Makro erstellen" auf, dann wird er zunächst aufgefordert, die Startobjekte einzugeben. Für unser Höhenschnittpunkt-Makro klicken wir also die Punkte A, B und C an. Danach sollen wir die Zielobjekte angeben: wir klicken auf den Höhenschnittpunkt H - und bis auf ein wenig Verwaltungsarbeit (Makronamen wählen, Hilfetext verfassen) ist das Makro damit erstellt.
In EUKLID DynaGeo ist ein Makro eine Liste von Objektvorlagen ("Blueprints"), welche später, also zur Laufzeit des Makros, als Konstruktionsbefehle interpretiert werden. Während das Makro aufgezeichnet wird, erstellt das Programm diese Liste der Blueprints. Sicherlich sind nach den oben geschilderten Eingaben die aus den Punkten A, B und C abgeleiteten Objektvorlagen in der Makroliste abgespeichert, und auch die dem Punkt H entsprechende; aber woher "weiß" das Makro, wie der Zielpunkt aus den Startpunkten zu konstruieren ist?
Dies ermittelt das Programm, indem es die Verwandtschaftsbeziehungen zwischen den Objekten analysiert. Der Aufbau der Makroliste geschieht gemäß dem folgenden einfachen Algorithmus:
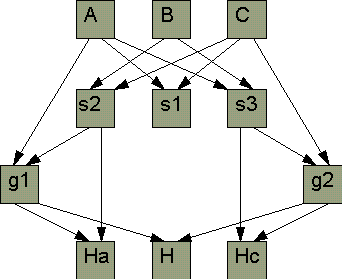
Nehmen wir unser obiges Beispiel wieder auf: Abbildung 10 zeigt die Verwandtschaften für die Objekte unserer Höhenschnittpunkt-Zeichnung.
Die Vorlagen für die drei Startpunkte werden also direkt in die Makroliste eingefügt. Wenn wir auf unser Zielobjekt, den Punkt H klicken, dann läuft gemäß dem obigen Algorithmus der folgende Vorgang ab:
Für H kann noch keine Vorlage ins Makro eingefügt werden, denn H ist ein Kind der Lotgeraden g1 und g2, und beide Geraden sind noch nicht in der Makroliste repräsentiert. Also werden zunächst diese Geraden bearbeitet:
nun sind auch alle Eltern von g1 verbucht, also kann eine Vorlage für g1 angefügt werden.
Als nächstes wird g2 bearbeitet: von den Eltern ist C schon verbucht, s3 aber noch nicht; also wird zunächst s3 bearbeitet:
nun sind auch alle Eltern von g2 verbucht, also kann eine Vorlage für g2 angefügt werden.
Schließlich sind jetzt alle Eltern von H verbucht, also wird der Makroliste eine Vorlage für den Zielpunkt H angefügt, und das Makro ist fertig.
Neben den Start- und den Zielobjekten enthält ein Makro also auch noch sogenannte "Zwischenobjekte"; im obigen Beipiel sind dies s2, s3, g1 und g2. Für das Makro überflüssige Konstruktionsteile werden automatisch übersprungen, wie z.B. die Lotfußpunkte Ha und Hc. Von jedem Zielobjekt aus wird das Netz der Verwandtschaften rekursiv zurückverfolgt, bis jeder dieser Pfade in einem Startobjekt endet. Dabei kommt man nur an solchen Objekten vorbei, die "echte Ahnen" der Zielobjekte sind.
Sollte einer der dabei verfolgten Pfade einmal in einem elternlosen Objekt enden, das nicht als Startobjekt aufgeführt wurde, dann bedeutet dies, dass die Makrokonstruktion inkorrekt ist, und der Anwender bekommt die Fehlermeldung, dass sich zumindest eines der Zielobjekte nicht aus den Startobjekten ableiten läßt.
Welche Daten enthalten denn nun eigentlich die "Objekt-Vorlagen", aus denen das Makro besteht? Für Startobjekte ist da im Grunde nur der Objekttyp nötig, damit zur Laufzeit des Makros entschieden werden kann, ob ein vom Benutzer angegebenes Startobjekt auch für dieses Makro paßt. Für Zwischen- und Zielobjekte muß darüberhinaus auch eine Liste der jeweiligen Eltern geführt werden, um zur Laufzeit die richtigen Verwandtschaftsbeziehungen zwischen den Objekten einrichten zu können.
Wenn das Makro schließlich angewendet wird, muß der Benutzer nur zu jeder der registrierten Startobjekt-Vorlagen ein passendes konkretes Objekt seiner aktuellen Zeichnung angeben. Nach den im Makro gespeicherten Vorlagen werden dann die Zwischenobjekte und schließlich die Zielobjekte erzeugt und gemäß den ebenfalls im Makro dokumentierten Verwandtschaftsbeziehungen miteinander vernetzt. Zwischenobjekte werden dabei verborgen; schließlich sollen dem Makroanwender ja gerade die ganzen Details der Konstruktion erspart bleiben!
E) Die Ortslinien
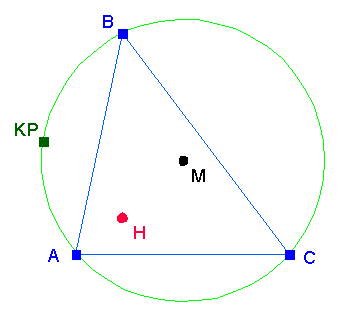
Das dritte charakteristische Kennzeichen dynamischer Geometriesoftware sind die Ortslinien. Betrachten wir als Beispiel die folgende Konstruktion:
 |
M ist ein freier Basispunkt |
An eine vorgegebene Kreislinie sind also die drei Punkte A, B und C gebunden; im Dreieck ABC ist sodann der Höhenschnittpunkt H konstruiert. Wenn man nun B auf dem Kreis entlang zieht, wie bewegt sich dann H?
In der einfachsten Version muß zur Beantwortung dieser Frage lediglich die Bahn des Punktes H aufgezeichnet werden, während B auf der Kreislinie entlanggezogen wird. Dazu wird in einem entsprechenden Ortslinien-Objekt eine Punktliste angelegt, in der die während des Zugvorganges aufeinanderfolgenden Lagen von H abgespeichert werden. Durch diese Serie von Punkten kann dann eine möglichst glatte Kurve gelegt werden (siehe Abbildung 12). Solch eine Kurve nennt man eine (statische) Spur des Punktes H.
Erheblich komplizierter wird das Problem, wenn man verlangt, dass die so aufgezeichnete Bahn des Punktes H in der Folgezeit am Zugmodus teilnehmen soll. In diesem Fall reden wir von einer "dynamischen Ortslinie". Dazu muß also die interne Punkteliste des Ortslinien-Objekts während des Zugvorganges mit aktualisierten Daten gefüllt werden.
Um zu verstehen, wie dies bewerkstelligt werden kann, müssen wir uns zunächst klar machen, von welchen Objekten die Ortslinie abhängt. Auf den ersten Blick scheint der einzige direkte Elter der Punkt H zu sein. Aber die Bahn von H hängt ja durchaus davon ab, welchen der beweglichen Punkte der Zeichnung man zieht, und auf welcher Kurve man ihn entlangführt. Wenn die Ortslinie von H aufgezeichnet wird, während sich B entlang des Kreises bewegt, dann nenne ich H den Generatorpunkt, B den Zugpunkt und den Kreis die Führungslinie. Generatorpunkt, Zugpunkt und Führungslinie sind sinnvollerweise als die Eltern der Ortslinie anzusehen.
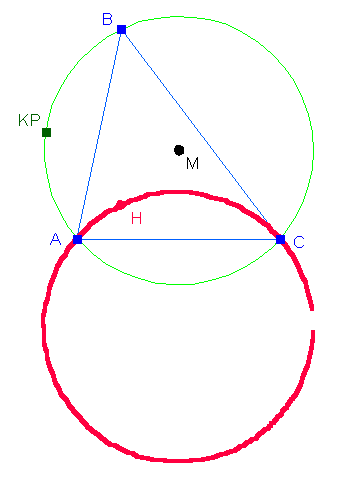
Was muß nun passieren, wenn man z.B. den Punkt KP ein Stück nach links zieht? Dabei wird der Kreis etwas größer, die Punkte A, B und C rutschen radial nach außen, die Dreiecksseiten werden nachgeführt, H wird neu berechnet, und schließlich bekommt die Ortslinie den Auftrag, sich zu aktualisieren, nämlich dann, wenn ihre drei Eltern (Zugpunkt, Generatorpunkt und Führungslinie) sich aktualisiert haben. Nun muß die Punkteliste mit neuen Daten gefüllt werden. Dazu muß der ganze Prozess der Ortslinienaufzeichnung intern nochmals durchgerechnet werden - mit der neuen Lage der Führungskurve! Also wird B intern auf dem nun vergrößerten Kreis entlanggeführt, wobei zu jeder Lage von B die zugehörige Lage von H ausgerechnet und in die Punkteliste der Ortslinie eingetragen wird.
Innerhalb des eigentlichen Zugvorganges, der ja an sich schon nicht gerade einfach ist, muß also nun noch die ganze Ortslinienaufzeichnung simuliert werden. Das Hauptproblem dabei ist, diese beiden Prozesse unabhängig voneinander zu halten. Die Details sind mühsam und kaum mehr allgemeinverständlich darzustellen, so dass ich es bei diesen prinzipiellen Überlegungen zum Problem der dynamischen Ortslinie bewenden lassen möchte.
Sie sollten als Anwender allerdings nie vergessen, dass die angezeigte Ortslinie stets nur eine numerische Approximation der wahren Bahnkurve des Generatorpunktes ist. Zwar sind die Stützpunkte exakt (soweit man das von den Ergebnissen eines numerisch arbeitenden Geometrieprogramms überhaupt sagen kann). Wenn aber die wahre Bahnkurve nicht genügend glatt verläuft oder die Stützpunkte zu weit auseinander liegen, kann die Kurvenapproximation gründlich schief gehen.
F) Zurück zum Geometrieunterricht
Nach diesen vielen programminternen Strukturen und Algorithmen dynamischer Geometriesoftware möchte ich zum Schluß noch ein Beispiel für einen meiner Meinung nach sinnvollen Einsatz eines DGS vorstellen. In diesem Zusammenhang möchte ich nochmals an die eingangs angeführten Regel erinnern, gemäß der der Computer nur eingesetzt sollte, wenn man mit seiner Hilfe etwas erreichen kann, das man ohne ihn nicht oder nur sehr viel schwerer erreichen könnte.
In meinem eigenen Unterricht habe ich ab und an das Problem, dass sich meine Schüler über einen speziellen geometrischen Sachverhalt nicht so sehr wundern, wie dieser es meiner Pädagogenmeinung nach verdient hätte. Da schneiden sich die drei Winkelhalbierenden in einem Dreieck in einem Punkt - und meine Schüler führen auf Nachfrage zur Begründung an, dass das ja auch bei den Mittelsenkrechten schon so war! Ein Grund für diese Unempfindlichkeit dem Besonderen gegenüber ist, dass das Normale viel zu selten erlebt wurde. In der Tat ist eine Konfiguration von drei Geraden, die sich in drei Punkten schneiden und sonst keine weiteren Spezialitäten bieten, keinem Mathematiklehrer auch nur zwei Minuten Unterrichtszeit wert.
Setzt man im Unterricht ein DGS ein, dann kann man mit Hilfe des Zugmodus in kurzer Zeit so viele verschiedene Varianten einer Konstruktion herstellen und studieren, dass man eine reelle Chance hat, das Besondere auch als eben ein solches erfahrbar zu machen. Der Trick ist: man beginne wenn möglich mit dem Normalen!
 |
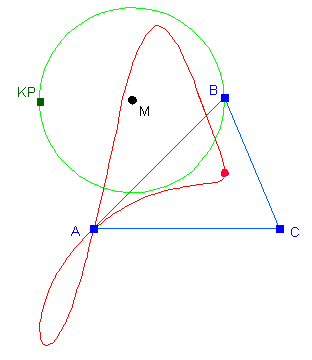 |
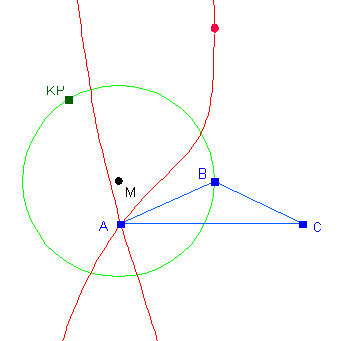
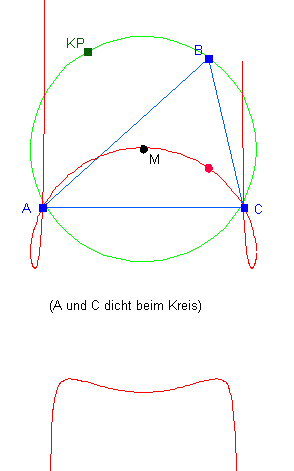
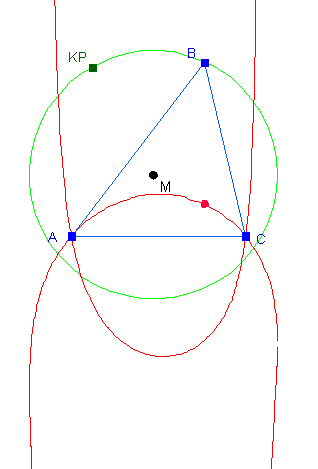
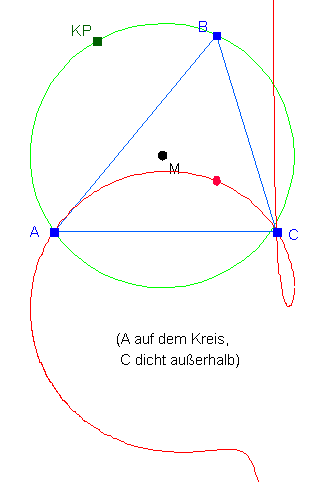
Wenn man z.B. die im vorigen Abschnitt vorgestellte Ortslinie des Höhenschnittpunktes eines Dreiecks im Unterricht behandeln will, dann wäre es doch schön, wenn die Schüler die Tatsache, dass diese Ortslinie ein Kreis ist, als etwas Besonderes erfahren könnten. Um dies zu erreichen, darf man keinesfalls mit der obigen speziellen Zeichnung anfangen; geht man von der etwas allgemeineren Fragestellung aus: "Wie bewegt sich der Höhenschnittpunkt eines Dreiecks, wenn sich eine Ecke des Dreiecks auf einem Kreis bewegt?", dann ergibt sich ein weiter Freiraum für Experimente. Ein paar Beispiele für solche Ortslinien sind in den folgenden Abbildungen zu sehen:
 |
 |
 |
Und dann zum Schluß natürlich auch:
Ein solches mathematisches Experiment ist ohne den Computer kaum durchführbar. Erst das dynamische Geometrieprogramm ermöglicht es, eine ganze Klasse von Kurven zu studieren. Und die meisten Ihrer Schüler werden es Ihnen danken, wenn sie einmal selbst forschend aktiv werden dürfen. Probieren Sie es aus!